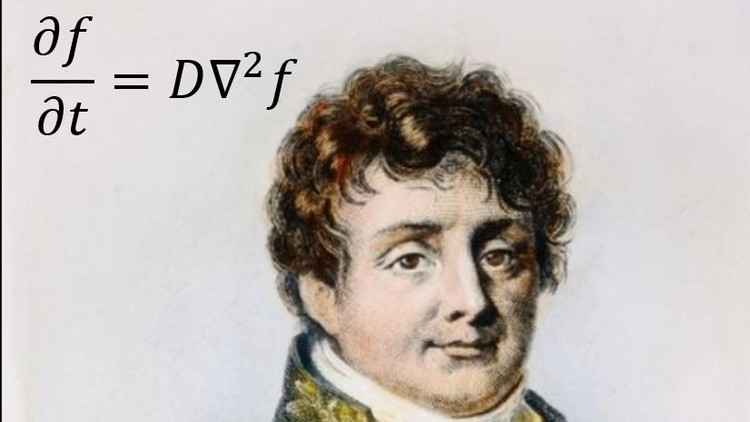
PDE solved by Fourier Transform, Fourier Series, method of separation of variables + section on uncertainty principle
What you will learn
How to use the Fourier Trasforms to tackle the problem of solving PDE’s
Fourier Transforms in one and multiple dimensions
Method of separation of variables to solve the Heat equation (with exercises)
Method of separation of variables to solve the Laplace equation in cartesian and polar coordinates (with exercises)
How to apply the Fourier Transform to solve 2nd order ODE’s as well
concept of streamlines
Mathematical tricks
How to derive Heisenberg Uncertainty Principle using concepts of Probability Theory
Description
The first part of the course aims to show how the Fourier Transform (FT) can be a powerful tool to solve Partial Differential Equations (PDE). The FT and its inverse (Inverse Fourier Transform, or simply IFT), are derived from the concept of the Fourier series at the beginning of the course, therefore it could be helpful to the student to already know the basics of such subject.
Calculus and Multivariable Calculus are a necessary prerequisite to the course, especially the topics related to: calculation of derivatives and integrals, how to compute the gradient, the Laplacian of a function, spherical coordinates, the calculation of the Jacobian, etc.
Some knowledge of residues used in Complex Calculus might be useful as well.
The second part of the course introduces the heat equation and the Laplace equation (in Cartesian and polar coordinates), and aims to show how to solve some exercises on PDE’s step-by-step. The exercises contain different boundary conditions and all the steps leading to the solution are motivated. The method that is used in the second part is that of Separation of Variables, which allows the PDE to be transformed in two different ODE’s (ordinary differential equations). This second part of the course is self-contained and independent of the first one. Some pre-requisite knowledge about ODE’s could be very useful.
Exercises on nonhomogeneous heat equations have also been added, as well as exercises on the Wave equation.
Another section to the course deals with the Diffusion/Heat equation. This equation is first derived from Physics principles described in the language of mathematics, then it is rigorously solved.
Bonus sections: These sections revolve around the mathematical derivation of Heisenberg Uncertainty Principle. Starting from some intuitive assumptions about probability distributions, we will derive this famous principle (which becomes a theorem starting from the axioms of probability). We will also dedicate some time to the physical insights and implications of this principle, such as the possibility that particles can come into existence and fall back into non-existence.
The prerequisites to this section are:
-knowledge of what probability distributions are
-how to calculate the mean and the variance of a random variable from a probability distribution
-the definition of the Fourier Transform and its Inverse Transform
-integration by parts and how to take derivatives
Content