Master Statistical Inference & Hypothesis Testing for Data Science: P-values, Confidence Intervals, A/B Testing Sampling
⭐ 1.00/5 rating
👥 1,132 students
🔄 October 2025 update
Add-On Information:
Note➛ Make sure your 𝐔𝐝𝐞𝐦𝐲 cart has only this course you're going to enroll it now, Remove all other courses from the 𝐔𝐝𝐞𝐦𝐲 cart before Enrolling!
- Course Overview
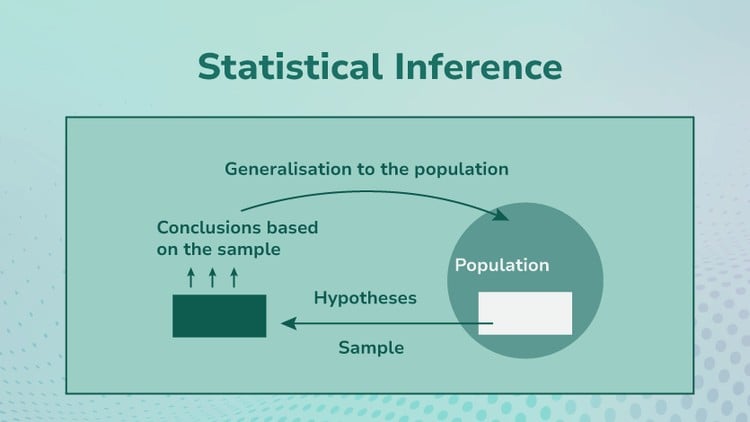
- Master the foundational principles of statistical inference and hypothesis testing, crucial for data scientists.
- Learn to transition from descriptive data summaries to drawing actionable, evidence-based conclusions from samples.
- Develop the ability to quantify uncertainty, enabling statistically sound decision-making in diverse data science projects.
- Understand the critical role of statistical rigor in experimental design, including the methodologies for effective A/B testing.
- Grasp core statistical concepts like probability distributions, the Central Limit Theorem, and the distinction between populations and samples.
- Explore various types of statistical errors (Type I and Type II) and learn to assess the power of a test.
- Focus on the practical application of statistical methods, translating theoretical knowledge into real-world data science solutions using Python.
- Demystify complex statistical jargon, building a robust analytical framework for confident data interpretation.
- Prepare thoroughly for advanced topics in machine learning, where statistical inference is vital for model validation and causal analysis.
- Requirements / Prerequisites
- A basic understanding of mathematics (algebra) is recommended to follow statistical derivations and formulas.
- Familiarity with elementary probability concepts (e.g., events, random variables) will be beneficial but not strictly necessary.
- Some exposure to fundamental data analysis concepts and data structures will aid in quicker comprehension.
- Basic programming knowledge in Python is required for understanding and implementing the practical coding examples.
- No prior advanced statistics, machine learning, or deep programming expertise is necessary; this course builds foundational skills.
- Access to a computer with a stable internet connection is required for lectures, materials, and hands-on coding.
- Guidance for setting up the necessary software environment, including Python with Anaconda and Jupyter Notebooks, will be provided.
- A proactive approach to learning and willingness to engage with practical exercises are key to success.
- Skills Covered / Tools Used
- Statistical Inference: Master point estimation and construct reliable Confidence Intervals for means, proportions, and differences.
- Hypothesis Testing: Formulate robust null and alternative hypotheses, select appropriate tests (e.g., Z-tests, t-tests, Chi-squared, ANOVA).
- P-value Interpretation: Accurately interpret p-values, significance levels (alpha), statistical power, and effect size.
- A/B Testing & Experimental Design: Design, execute, and analyze controlled experiments, including multi-variate testing principles.
- Sampling Methodologies: Understand sampling distributions, apply the Central Limit Theorem, and differentiate various sampling techniques.
- Data Visualization: Utilize Python libraries for effective visualization of data distributions, test results, and inferential findings.
- Python for Statistics: Gain proficiency with NumPy, Pandas, SciPy, Matplotlib, Seaborn, and especially StatsModels for advanced statistical analysis.
- Interactive Computing: Leverage Jupyter Notebooks for an interactive and reproducible statistical analysis workflow.
- Non-Parametric Tests: Introduce methods like Mann-Whitney U and Wilcoxon signed-rank for non-normally distributed data.
- Common Pitfalls: Learn to identify and mitigate common errors and biases in statistical analysis and experimentation.
- Benefits / Outcomes
- Confidently interpret statistical findings from your datasets, drawing clear and accurate conclusions.
- Make statistically sound, evidence-based decisions in your data science projects, enhancing reliability.
- Design, implement, and analyze robust A/B tests for optimizing product features, marketing, and user experience.
- Critically evaluate research and industry reports for statistical validity, identifying strengths and weaknesses.
- Effectively communicate complex statistical insights to both technical peers and non-technical business stakeholders.
- Avoid common statistical fallacies and misinterpretations (e.g., p-hacking), ensuring integrity in your analysis.
- Build a strong foundation crucial for advanced machine learning model validation, evaluation, and causal inference.
- Enhance your problem-solving abilities by integrating rigorous quantitative methods into your analytical workflow.
- Boost your career prospects in highly sought-after data science, analytics, and research roles across various industries.
- Develop a data-driven mindset, enabling you to advocate for and implement evidence-based strategies.
- PROS
- Comprehensive and practical coverage of essential statistical inference and hypothesis testing concepts.
- Strong emphasis on hands-on Python implementation, ensuring direct applicability to real-world data science challenges.
- Accessible for beginners with clear, step-by-step explanations, making complex topics digestible.
- Directly teaches crucial industry skills like A/B testing and experimental design, highly valued in modern data roles.
- Fosters critical thinking about data evidence, empowering more informed and reliable decision-making.
- Provides a robust foundation for pursuing more advanced analytical and machine learning studies.
- Empowers data scientists to make confident, evidence-based contributions to business strategy.
- CONS
- Requires consistent intellectual effort and dedicated practice to fully internalize the underlying mathematical principles and statistical reasoning.
Learning Tracks: English,IT & Software,Other IT & Software
Found It Free? Share It Fast!