Riemann surfaces and their applications in integrable system

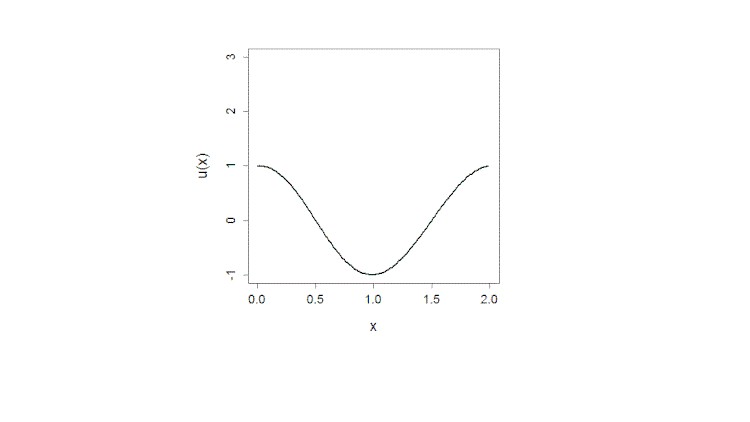
In this course we discuss very interesting and beautiful object – Riemann surfaces. Riemann surfaces have many different applications in integrable systems. And one of our main aim is to explain how Riemann surfaces and their degenerations in singular algebraic curves help to solve problems from geometry and integrable models of mathematical physics. For example, one of such models is a famous Korteweg-de Vries equation:

ut = (6 u uxx +uxxx )/4, u = u(x, t).

This equation describes solitons, that is, solitary water waves in a channel. The theory of Riemann surfaces and its applications in integrable models of mathematical physics.

Sincerely, Andrey Mironov.

Описание курса на русском языке:

В этом курсе мы обсуждаем очень интересные и красивые объекты – римановы поверхности. Римановы поверхности имеют много различных применений в интегрируемых системах. И одна из наших главных целей-объяснить, как римановы поверхности и их вырождения в сингулярных алгебраических кривых помогают решать задачи из геометрии и интегрируемых моделей математической физики. Например, одной из таких моделей является знаменитое уравнение Кортевега-де Фриза:

ut = (6 u uxx +uxxx )/4, u = u(x, t).

Это уравнение описывает солитоны, то есть одиночные волны воды в канале.

Теория римановых поверхностей и ее приложения в интегрируемых моделях математической физики. Мы будем рады видеть Вас на нашем курсе!

Приятного изучения.

С уважением, Андрей Миронов.