Learn calculus 1 part 4

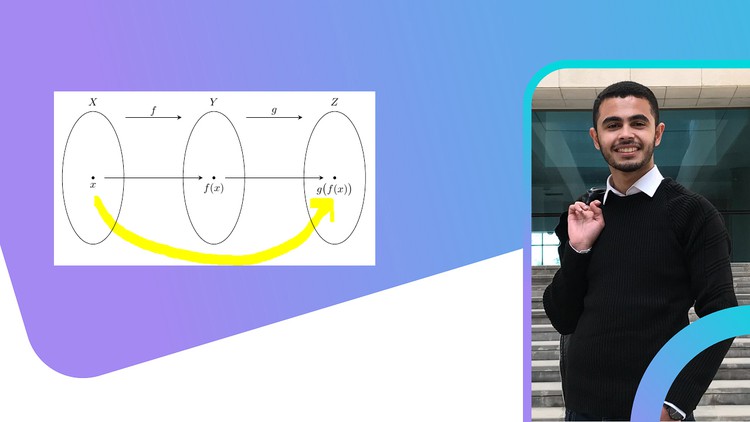
In mathematics, function composition is an operation that takes two functions f and g and produces a function h such that h(x) = g(f(x)). In this operation, the function g is applied to the result of applying the function f to x. That is, the functions f : X → Y and g : Y → Z are composed to yield a function that maps x in X to g(f(x)) in Z.

The composition of functions is always associative—a property inherited from the composition of relations.

That is, if f, g, and h are composable, then f ∘ (g ∘ h) = (f ∘ g) ∘ h. Since the parentheses do not change the result, they are generally omitted.

In a strict sense, the composition g ∘ f is only meaningful if the codomain of f equals the domain of g; in a wider sense, it is sufficient that the former be a subset of the latter.

Moreover, it is often convenient to tacitly restrict the domain of f, such that f produces only values in the domain of g. For example, the composition g ∘ f of the functions f : ℝ → (−∞,+9] defined by f(x) = 9 − x2 and g : [0,+∞) → ℝ defined by {displaystyle g(x)={sqrt {x}}} can be defined on the interval [−3,+3].

Compositions of two real functions, the absolute value, and a cubic function, in different orders, show a non-commutativity of composition.

The functions g and f are said to commute with each other if g ∘ f = f ∘ g. Commutativity is a special property, attained only by particular functions, and often in special circumstances. For example, |x| + 3 = |x + 3| only when x ≥ 0. The picture shows another example.

The composition of one-to-one (injective) functions is always one-to-one. Similarly, the composition of onto (surjective) functions is always onto. It follows that the composition of two bijections is also a bijection. The inverse function of a composition (assumed invertible) has the property that (f ∘ g)−1 = g−1∘ f−1.

Derivatives of compositions involving differentiable functions can be found using the chain rule. Higher derivatives of such functions are given by Faà di Bruno’s formula.